定义
我们首先来看一条公式:
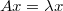
这时,我们可以把λ称为矩阵A的特征值,把x称为矩阵A的特征向量。我们也可以这么说,Ax与x方向平行,而λ是x的长度伸缩大小。同时还有一点需要提起,就是λ可以为0,这时就转换成了Ax=0的问题,也就是求A的零空间了,即其零空间的向量都是λ=0时的特征向量。不过,零向量一般不考虑为特征向量,因为没意义。
比如说下图,AB=(1,1)为矩阵A的特征向量,其特征值为3。
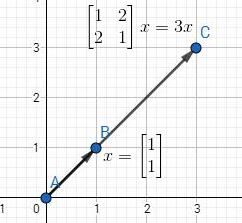
回顾下之前的投影矩阵,如果向量b刚好处在矩阵A的列空间上,那么对于矩阵A的投影矩阵P有:Pb=b(想象平面上的线被投影多少次都是本身)。那么b就是P的特征向量,1为其特征值。
那么当向量b'正交于矩阵A的列空间,那么有:Pb'=0=0*b'。那么b'是P的特征向量,0为其特征值。
故对投影矩阵而言,其特征值为0和1。
对于特征值而言,其跟矩阵的迹和矩阵的行列式和有密切的联系,即特征值和为矩阵的迹的和,特征值的乘积为矩阵行列式的值,具体的论证过程可看番外篇 · 矩阵的迹&行列式值&特征值三者关系。
如何求解
我们可以将Ax=λx装化成(A-λI)x=0。因为x有解,所以可以得知A-λI的行列式为0,因为对于n*n的矩阵而言只有奇异矩阵其零空间才有除零向量外的值(奇异矩阵即不满秩的矩阵,其行列式为0,因为最后总可以靠消元法让最后一行全为0,而有一行0的行列式其值为0)。这时,就转为求|A-λI|=0的λ解了,当λ求出后即可代入(A-λI)x=0转而求出特征向量x的值。下面举个具体的计算例子,求矩阵A的特征向量和特征值:
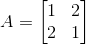
首先计算|A-λI|=0的值:
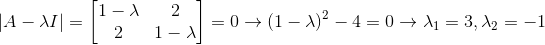
得到两个λ后分别代入原式求特征向量:
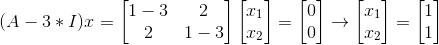
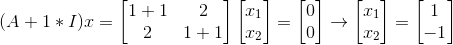
这时就求出两组特征值和特征向量了:
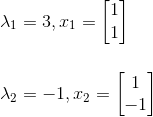
这时,有个问题,如果特征值不同,那么其各自对应的特征向量可能存在线性相关么?
答案是否,特征值不同的特征向量线性无关。证明如下:假定有k个线性无关的特征向量与其对应的不同特征值,那么如果存在不同的特征值,其特征向量与之前k个特征向量线性相关,那么得到式子1:
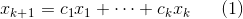
将式子1两边都左乘矩阵A,根据Ax=λx可得式子2:
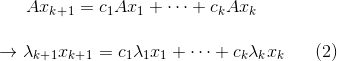
将式子1两边都乘以λk+1得到式子3:
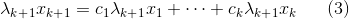
将式子2减去式子3可得式子4:
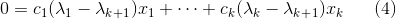
结合式子4,因为已知前k个特征向量线性无关,又k+1个λ都不相同,那么只有c变量都为0时式子4才成立。而c全为0代表k+1个特征向量线性无关,所以之前的假设不成立,所以特征值不同,其特征向量线性无关!
那么问题又来了,因为λ可以重复出现,如果λ只出现一次,那么其可能存在两组线性无关的特征向量么?
答案依然是否,因为假如一个n维矩阵有n个不同的λ,那么根据刚刚推导可知这n个λ推出的特征向量线性无关,那么假如一个λ可以推出两个线性无关的特征向量,那么特征向量的维数就大于n维了,这是不可能存在的,所以总的来说,一个特征值对应一个特征向量,不过特征值可以重复出现,但每一个重复出现的特征值都只能对应一个线性无关的特征向量。
打个比方,如果我有一个3维的矩阵,其只有两个不同的特征值λ1和λ2,但λ1可以算出有两组线性无关的特征向量,这时就相当于特征值有三个——λ1,λ1,λ2,分别对应三组线性无关的特征向量。(注意,一个特征值只能有一个线性无关的特征向量,如果一个特征值推出两个,那么就追加一个同等特征值来与之对应)。
马尔科夫矩阵
各位或许会困惑为什么突然提到马尔科夫矩阵吧,因为它能用特征向量来解释。什么叫马尔科夫矩阵?其具有两个重要的性质:
1. 其内所有元素都大于等于0
2. 所有列向量自身元素和为1
举个简单的例子:
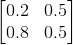
其中,可推导出两个性质:
1. 其有一个为1的特征值
2. 其他特征值的绝对值都小于1
我们先来看下如何证明第一个性质:
首先有一个马尔科夫矩阵A:
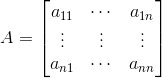
将λ=1代入|A-λI|得:
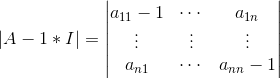
将行列式的第一行加上其余剩下的所有行,其行列式不变(根据行列式性质5):
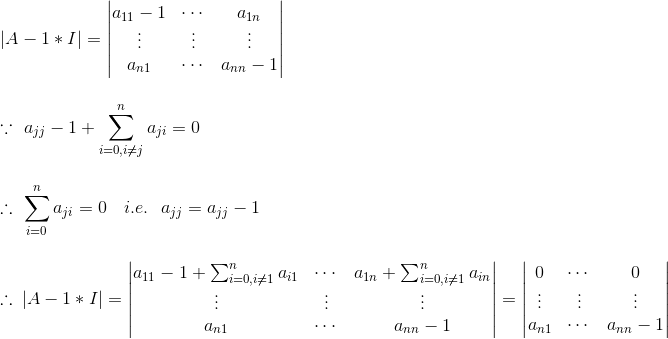
因为首行都为0,所以很容易知道其行列式为0(根据行列式性质6):
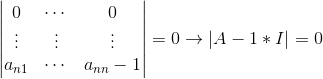
所以可以得知1为矩阵A的一个特征值。
那么接下来证明性质二,其他特征值绝对值都小于1:
在证明这个问题前,先提出一个问题,如果A是马尔科夫矩阵,那么A*A是不是仍然是马尔科夫矩阵,A*A*A呢?
答案是肯定的,以A*A为例:
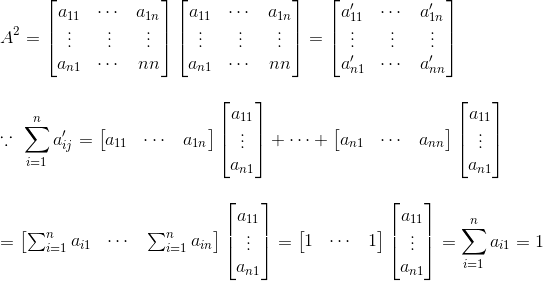
所以A*A的每个列向量自身和为0,且每个元素都大于0,所以A*A为马尔科夫矩阵,同理A*A*A也是,A的n次方都是马尔科夫矩阵。
回到一开始的证明,如何证明马尔科夫矩阵除了特征值为1外其余特征值绝对值都小于1。这里需要利用特征分解:
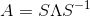
那么有(证明过程见特征分解):
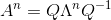
因为A的n次方是马尔科夫矩阵,所以其元素都小于等于1,如果|λ|>1,那么Λ里就有元素会无限大,这与等式不符,所以有|λ|<=1。
综上可以得到马尔科夫矩阵的4条性质:
1. 其内部全部元素都大于等于0
2. 其每列元素相加都等于1
3. 其一定有一个特征值等于1
4. 其除了等于1的特征值外其余特征值绝对值都小于1
马尔科夫矩阵应用
举一个简单的例子,假设有两个盒子A和B,其每个盒子里初始小球都为100个,每次盒子A中有20%的小球转移到盒子B中,而盒子B有40%的小球转移到盒子A中,问经过n次后,盒子A和B各剩下几个球?
我们可以先将该问题转化成马尔科夫矩阵来解决,第n次A和B的值与第n-1次有关:
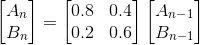
先求出该马尔科夫矩阵的特征值和特征向量:
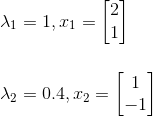
因为两个特征向量线性无关,所以我们可以将初始状态的AB用两个特征向量表示:
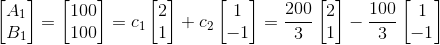
将马尔科夫矩阵定义为矩阵P,有:
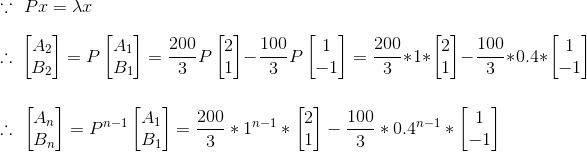
当n趋向无穷大时,只有λ=1的那部分留下来,另一部分由于太小被舍弃,所以最终可得:
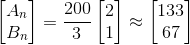
所以最终A箱子有133个小球,B箱子有67个小球,无论再进行再多少次转换都不变,这就形成一个稳态。
而马尔科夫矩阵最后都能得到一个稳态,因为其具备一个等于1的特征值以及绝对值小于1的其他特征值。那我们现在从稳态出发,已知状态n已经达到稳态了,那么继续马尔科夫过程会有什么样的结果?

这不就是求马尔科夫矩阵当λ=1时的特征向量的方程么?
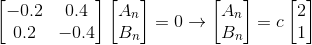
所以我们很容易就能得到稳态时A,B的比例=2:1,因为总量是200,所以A剩下400/3,B剩下200/3,与之前计算出的结果一致。所以只要有一个马尔科夫矩阵,其λ=1时的特征向量的比例就是稳态时的比例。
好了,马尔科夫矩阵先介绍到这,下一节介绍特征向量的另一种应用:特征分解