十大属性
行列式首先要了解的是其十大属性:
1. 单位矩阵的行列式值为1,记为:
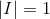
2. 在行列式里,交换行会改变其正负性,即每换一行其值正负交换一次,举例:
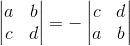
3. 行列式里的每一行单独(注意是单独一行)具有线性性质,举例:
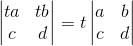
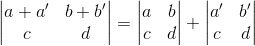
4. 如果行列式里有两行相等,那么其行列式为0,举例:
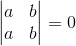
证明:如果有两行相等,那么交换并不会改变该行列式,但性质2表明其会换号,所以只能为0。
5. 行列式第k行加上第i行的j倍,其值不变,举例:
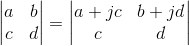
证明:可以利用性质3将行列式拆开,再利用性质4得到最终结果:
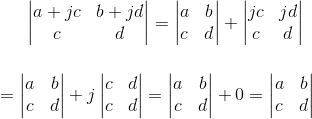
6. 如果行列式有一行全为0,那么该行列式值为0,举例:
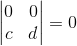
证明:可以利用性质3将行列式拆开,0乘以任何数都为0:
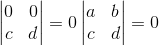
7. 三角矩阵其行列式值为对角线上的值的乘积,举例:
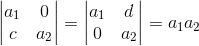
证明:可以利用性质3先用消元法将矩阵转换成对角矩阵,其行列式值不变,然后利用性质3把对角线上的值提取出来:
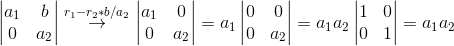
8. 当矩阵是奇异矩阵(奇异矩阵就是矩阵秩小于n的n阶方阵)时,其行列式为0;当矩阵可逆时,其行列式不为0。
证明:当矩阵是奇异矩阵时,肯定能通过消元转换成有一零行的存在,所以行列式为0;当矩阵可逆时,相当于矩阵秩等于n的n阶方阵,其不可能转换成有零行的存在,对角线上也不可能出现0,所以不为0。
9. AB的行列式等于A的行列式乘以B的行列式:
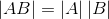
这时有些例子需要说明下:
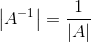
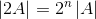
10. A的行列式等于A转置的行列式:
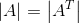
证明:可以利用LU分解,由于三角矩阵行列式只跟对角线有关,所以:
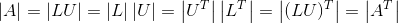
行列式计算
那么行列式该如何计算?我们可以利用消元法将原先矩阵变成三角矩阵后,其对角线上的元素的乘积就是其行列式的值。
此外,我们还有一种通用的行列式求值公式,我们先来看下一个2*2的行列式求值:
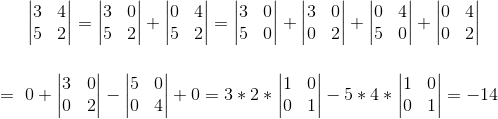
我们通过刚刚的推导,可以推出n维的行列式的求值,就是不断把原来行列式拆成单元矩阵I后再进行运算。且同时发现,不同行的元素肯定不能处在同一列,因为这会出现一整列为0的情况导致整个行列式为0,所以不同行的元素得处在不同列上。
那么,这里有个问题,n维的行列式其总共有多少个不为0的子行列式组合?答案是n!个,因为我们首先可以确定第一行不为0的元素的位置,总共有n个位置,接下来确定第二行,n-1个位置,第三行n-2个位置,第n行只有一个位置,全部相乘就是n!。
这时我们可以推出一个一般公式,假定有一n*n的矩阵A:
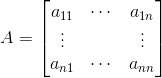
其行列式的值为:
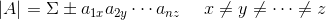
其中,正负号视具体情况而定。
除此之外,还有另外一种通用的方法,就是行列式展开,这方法基于刚刚那种做法,只是把公式里的数字转换成行列式的形式,这里我不再赘述了,直接引用维基百科:


行列式不多讲,下一节讲讲特征值和特征向量。