定义
我们首先来看一条公式:
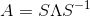
其中S由n个线性无关的特征向量组成,Λ为λ组合成的对角矩阵。这条公式在图像处理中十分有用,举个例子如图片的压缩(具体步奏以后会讲)。但是要注意的一点是,并不是所有的矩阵都能特征分解,所以其存在局限性,后面会讲SVD(奇异值分解)就更显优势,应用范围也更广,不过都是后话了,这节重点还是特征分解。
公式从何来?
我们先假定有一个n*n的矩阵A,其有n个线性无关的特征向量,将其组合成S=[s1,s2,……,sn](注意s为列向量),那么有:
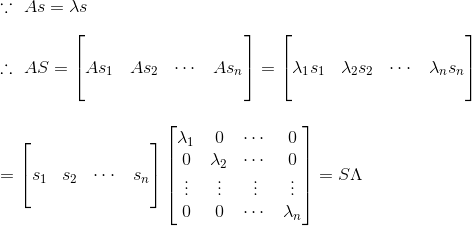
那两边各右乘S的逆可得:
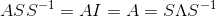
当然,两边可以各左乘S的逆,那么可得:
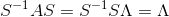
而这种叫做将矩阵A对角化。
另外还有一点需要提醒的是,λ值可以重复,但特征向量一定要有n个线性无关才行。
公式的简单应用
已知A有n个线性无关的特征向量,那么A^100等于多少?
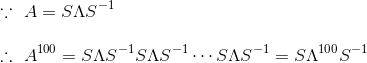
由于Λ是对角矩阵,所以100次幂也很好求:
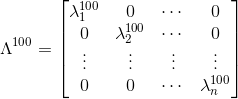
公式的变体
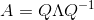
其中A是一种特殊的矩阵——对称矩阵,Q仍然是矩阵A的特征向量组合成的矩阵,但其具有正交性。具有正交性也就意味着Q的逆等于Q的转置,所以有了最终的公式:
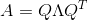
当然,这条公式只有当矩阵A是实对称矩阵才永远成立。那什么是实对称矩阵,当A的转置等于A本身时,A称为对称矩阵,当A所有的元素都为实数,那么A就是实对称矩阵。那为什么实对称矩阵A具有这种性质?
首先来看下实对称矩阵的性质一:其所有特征值都是实数,对应的特征向量也都是实向量;
假定有一n*n的矩阵,有:
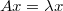
两边同时取共轭,可得:
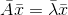
什么叫共轭?
一般来说共轭指的是共轭复数,利用维基上的一张图来解释下:

如图中Z和Zbar就是一组共轭复数,就是实部保留不变,虚部变号,实数的共轭复数是其本身:
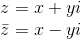
举例说明:
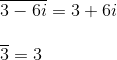
一般共轭复数满足加减乘除运算:
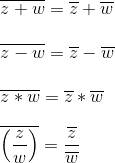
回到刚刚那个证明上,等式两边同时取转置可得:
一般来说共轭指的是共轭复数,利用维基上的一张图来解释下:

如图中Z和Zbar就是一组共轭复数,就是实部保留不变,虚部变号,实数的共轭复数是其本身:
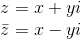
举例说明:
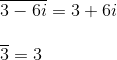
一般共轭复数满足加减乘除运算:
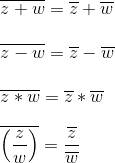
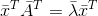
因为矩阵A是实对称矩阵,所以有:
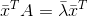
两边同时右乘x得:
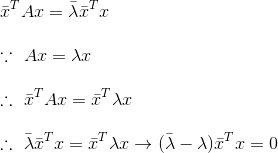
其中:
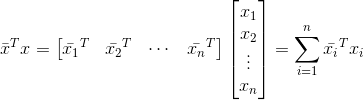
假设xi的实部是a,虚部是b:
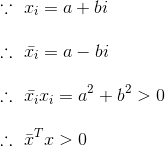
所以有:
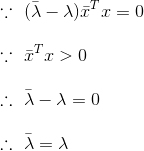
因为λ的共轭复数等于本身,所以λ是一个实数。因为λ都是实数,所以(A-λI)的元素都是实数,其(A-λI)x=0的解x也都是实向量,所以其特征向量都是实向量。
知道这个重要的前提后,我们来推导第二条性质,实对称矩阵的特征向量相互正交,也可以说实对称矩阵可以被正交对角化。
假定矩阵A有两个不同的特征值λ和u,其特征向量为x和y:
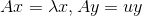
将Ay=uy等号左右各取转置可得:
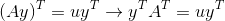
因为A为对称矩阵,所以A的转置等于A:
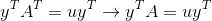
等号两边同时乘以x可得:
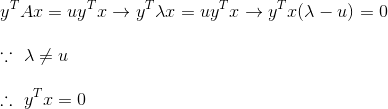
所以最后可得x和y正交,拓展开来就是其所有特征向量都相互正交。
综上,利用本节最开始的特征分解公式,对称矩阵的分解就是正交分解,其公式为:
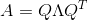
最后再聊点对称矩阵的特殊性质:
1. 对称矩阵可看成是相互正交的投影矩阵的组合。
对于对称矩阵A而言,其正交分解可以继续分解成多项式:
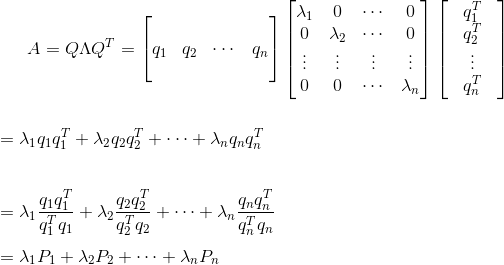
因为特征向量具有正交性,所以向量q的转置与q相乘为1,以1为分母并不会改变等式,这就让多项式变成了多个正交的投影矩阵P的组合。比如其中第一个就是λ1乘以q1的投影矩阵。
2. 对称矩阵主元(pivot)中大于0的个数跟其特征值里大于0的个数是一样的。举个例子,对于矩阵A而言:
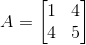
将其消元得到两个主元——1和-11:
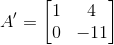
其中主元正的有1个,值为1,负的有1一个,值为-11。那么其特征值为:
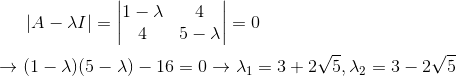
其中λ1>0,λ2<0,跟主元一致。具体的验证方法目前没时间写,以后再看看。
另外还有一点,主元的积就是矩阵A的行列式值,而特征值的乘积刚好也是矩阵A行列式值(证明方法可看番外篇 · 矩阵的迹&行列式值&特征值三者关系),所以主元的乘积也是特征值的乘积。
3. 任意n*n的实对称矩阵都有n个线性无关的特征向量。具体验证方法以后再补充~
下一章节,实对称矩阵进阶版——正定矩阵。