定义
我们首先来看什么叫正定矩阵。标题已经很明确了,首先得是对称矩阵(下文中对称矩阵都指实对称矩阵)。其次,其还得具备以下4点中的任意一点(只要满足1点另外3点一定满足):
1. 所有特征值都大于0
2. 所有子行列式都大于0.这点我需要解释下,举个例子,一个3*3的矩阵A:

其子行列式定义为以下三种:
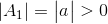
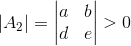

3. 其所有主元(pivot)都大于0(因为主元大于0的个数跟特征值大于0的个数是一致的,具体例子可见特征分解)
4. 对于所有可以相乘的x(满足矩阵运算条件的x,且x不等于0):
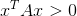
对于性质1.2.3是判定的标准,性质4是通过1.2.3推导而来,具体过程以后有空再补上~
详细介绍
我们来做进一步的剖析。假定一个矩阵A:
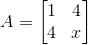
当x是多少时该矩阵A为正定矩阵?首先其是一个对称矩阵,接下来我们可以利用性质2,因为第一个子行列式为1大于0,第二个子行列式为x-16,也就是说当x>16时该矩阵就是正定矩阵。
换句话说,如果x>16,其一定有两个正的特征值。当x=16时,其有一个为0的特征值,另一个为正的,这时称该矩阵为半正定矩阵。当x<16时,其至少有一个负的特征值。
那我们假设x=16,这时通过性质4可得到一个多项式:
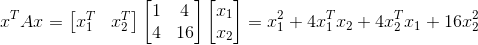
乍看下如果问你这个多项式有没有极小值,如果有是多少?这个肯定看不出,但是我们知道它是半正定矩阵推出的,所以其有极小值=0。我们也可以将多项式用配方法:
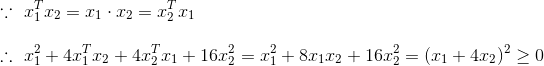
那么当x>16,假如x=17时该多项式为(当x1,x2都为0时才等于0):
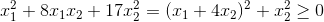
那么当x<16,假如x=15时,该多项式为:
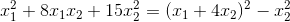
这时我们可以断定其没有极小值,因为其不是正定矩阵,或者说其配方后的结果可能出现负数。
所以我们可以配方法来判断二元函数的极小值,也可以通过正定矩阵来判断其极小值。
这时我们可以再仔细研究下配方法,其实其跟矩阵的消元法(或者说LU分解)有密不可分的联系。以x=17时的矩阵A为例:
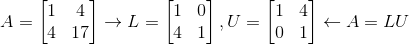
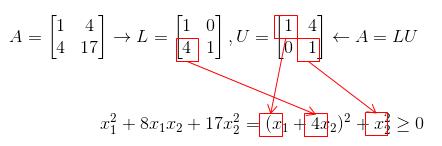
其中矩阵的主元分别是(x1+4x2)^2的系数和x^2的系数,而转换矩阵L中的转换率4则是(x1+4x2)中x2的系数。照此规律就可以推广到多元函数的配方。
另一方面,判断函数有没有极小值可以靠一阶导数为0,二阶导数>0来判断的。但放到矩阵中,就是靠二阶导数矩阵(或称为Hessian矩阵)的正定性来判断的。比如说一个二元函数 f(x,y),其二阶导数矩阵为:
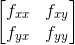
因为二阶导数fxy=fyx(简单解释下,先对x求导会将只有y部分消去,再对y求导会将x部分消去,那么剩下就是x和y共有的部分;这跟先对y求导消去x部分,再对x求导消去y部分得到的剩下部分一致),所以该矩阵为对称矩阵,只要其满足4条性质中的某条,那么就是正定矩阵,那么该二元函数f就有极小值。
A+B
那么再提个问题,如果A是正定矩阵,B也是正定矩阵,那么A+B是不是正定矩阵?
答案是肯定的。通过性质4可推导出:
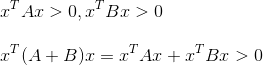
A转置乘以A
那对于任意m*n矩阵A,其转置乘以本身得到的结果是正定矩阵么?
我们可以利用性质4:
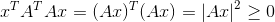
当A零空间只有零向量时,Ax>0,满足正定矩阵的要求,当A零空间维数大于0时,其Ax>=0,故是半正定矩阵。而这种产生正定矩阵的方法,在机器学习中十分常见,故最好记住其对应性质,以便以后使用~
下一章,奇异值分解——SVD基础篇