定义
我们先来看下奇异值分解的公式,对于任意矩阵A:
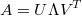
其中U和V都是单位正交矩阵,Λ是对角矩阵。
公式从何来?
我们先来看下矩阵有何线性意义。从第一章到现在已经写了近20篇有关矩阵的文章了,但是矩阵有没有直观点的表示形式呢?答案是有的,以下摘录了We Recommend a Singular Value Decomposition的内容。
我们先来看一个矩阵M:
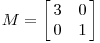
那这个矩阵对平面上的一个点(x,y)的影响是什么?在这之前,先来解释下向量(a,b)的定义,我们通常说的(a,b)是以(1,0)和(0,1)两个向量作为坐标的基底,如果我把基底变成(1,0),(0,3),那么(a,b)就不再是代表原来那个点了,而是原先坐标系的(a,3b),不过在转换后的坐标系上仍然写成(a,b)。理解了这点后,我们再来往下看:
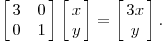
可以明显看出y不变,x被拉长了3倍。我们再来更具体的感受下这个矩阵的作用,假定原来坐标系里有一个1*1的正方体,经过这个矩阵的作用后,其变换成:
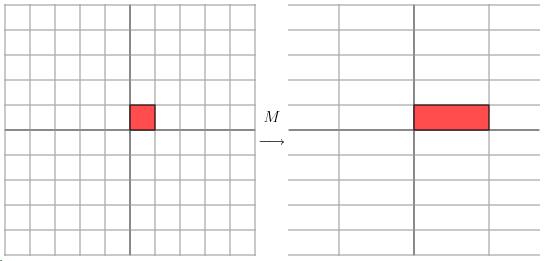
通过这个例子,我们些许能感受到正方形的变形,是由于基底(x,y)的变形(x向量的变形)。比如对于转换前的正方形,其顶点位置为(1,1),而转换后的顶点位置仍为(1,1):
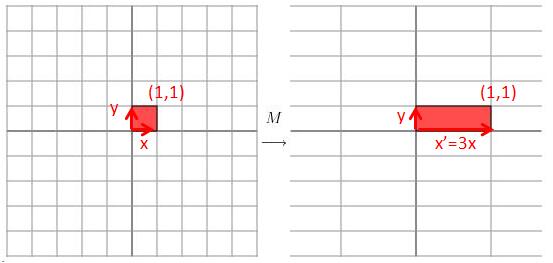
变化的只是基底。我们再来看另一个矩阵,同样命名为M:
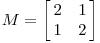
如果将其作用到刚刚的坐标系中,会有怎么样的变化:
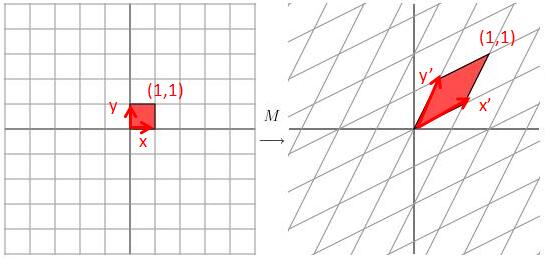
感觉没法怎么描述这个变化,因为基底x和y都发生了旋转拉伸。但是我们先将原来的坐标系逆时针旋转45度后,再经过矩阵M的变换,其结果为:
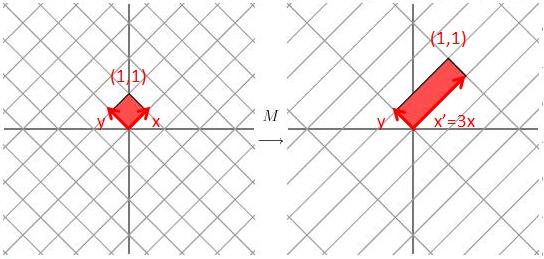
这时会惊喜发现这个变换跟刚刚那个一致,也是x方向拉长3倍,y方向不变。这时问题来了,仔细观察上面两个矩阵的变换能发现一个共同的特征,转换前后其基底都是正交的,那么对于任意矩阵M,是否总能存在一个本来正交的基底,转换后的基底也是正交的?
我们再来看一个例子:
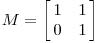
仍然放到一个普通的正交基底上时,可看到转换后的基底并不正交:
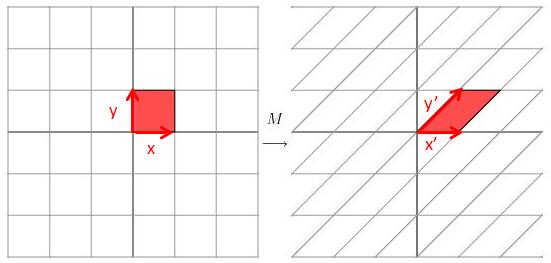
那我们先将原来的正交基底逆时针转30度,可得:
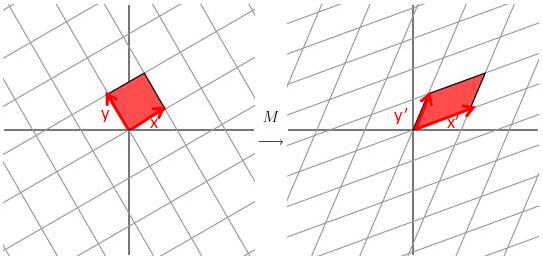
可以感觉基底逐渐朝正交的方向发展~我们继续选择原来的基底,这次逆时针转60度:
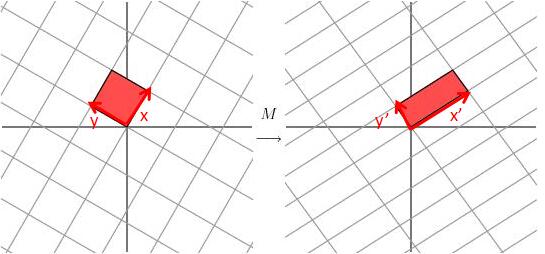
几乎正交了!最后,经过实验表明,正交需要的角度是58.28度。
有了上面三个例子做铺垫,下面我们直接从基底出发来分析这个问题,假定转换前基底正交:
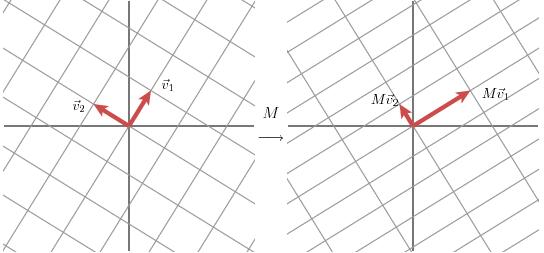
我们将转换后的基底单位化后,用u表示,有:
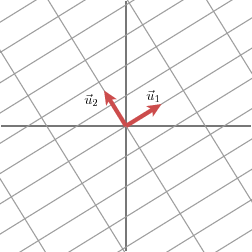
那么就有如下公式:
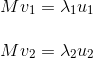
对于以v为基底的坐标轴,我们在中随意找个点X,其在v1方向的长度是v1·X(v1与X点乘),在v2方向的长度是v2·X(v2与X点乘),那么X可表示成如下形式:
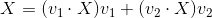
等号左右各乘以M可得:
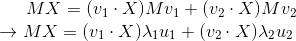
因为v1·X和v2·X是常数而不是矩阵,所以可以移到后面,而且点乘可以表示成转置乘,所以有:
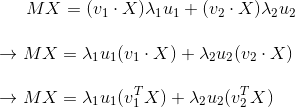
等号左右再右乘X的逆,可得:
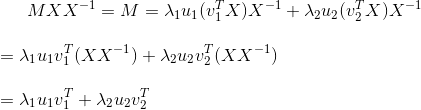
转换成矩阵的形式,就是:
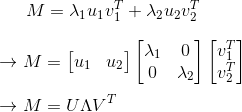
这就得到了SVD公式,那怎么证明u1,u2正交?我们可以通过证明(λ1u1)·λ2u2=0来证明其正交:
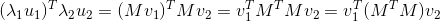
这时当v2是(M转置M)的特征向量时,公式可以继续推导下去:
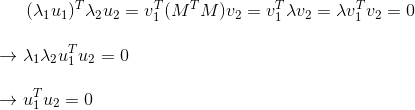
因此可以看出u1,u2也是正交的当v2为(M转置M)的特征向量。因为(M转置M)是对称矩阵,那特征向量可以相互正交(推导可参考对称矩阵的正交分解),那么v1也是(M转置M)的特征向量。
综上,对于任意矩阵A,找到(A转置A)的一组正交单位特征向量,可以通过矩阵A转换得到另外一组正交单位特征向量。
怎么求SVD
基于刚刚所说,我们也可以直接结合公式得到:
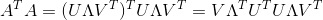
因为U是正交矩阵,所以U转置U=单位矩阵,有:
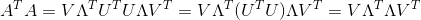
因为Λ是对角矩阵,所以其转置乘本身为其平方:
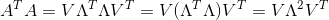
结合之前学过的对称矩阵的正交分解,可以很快求出V和Λ,这也可以说明上部分最后提到的限制条件——v是(A转置A)的一组正交单位特征向量。求出V和Λ后就可以求出U,求U有两种方法:
1. 跟求V一样,不过这次右乘A的转置:
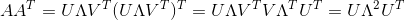
可见U是(AA转置)的特征向量。同时和V共享同个特征值(Λ^2)——AB的特征值与BA的特征值一致:
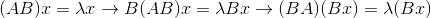
2. 由于Λ大多是对角矩阵,其逆就是对角元素的倒数的集合,所以直接通过公式计算就可以得出:
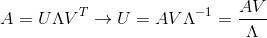
不过这方法并不是总能见效,如果Λ中对角线上有零元素出现的话,只能利用单位正交矩阵与格拉姆-施密特正交化来补充剩余的元素。
求SVD的例子
先来个简单的例子,有一矩阵A:
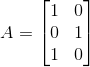
首先算A转置A的值:
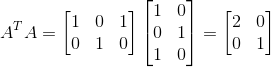
接下去算出其特征值和单位化后的特征向量:
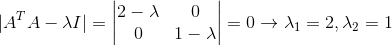
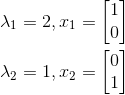
这时就知道Λ和V的值了,可以得出:
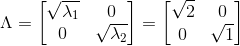
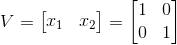
接下来算U,我们采用第一种方法,先算出(AA转置)的值,后再求其特征向量:
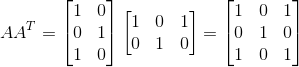
接下去算出其特征值和单位化后的特征向量,因为特征值与(A转置A一致),所以可以推出其特征值为:
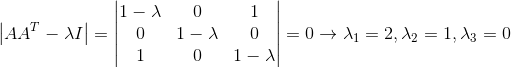
单位化后的特征向量为:
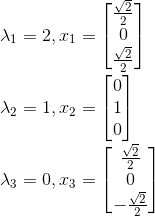
所以可以得知其U为:
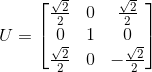
最后整合公式,得:
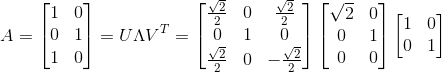
简单例子举完,下面我会举个复杂的例子,其参考了奇異值分解 (SVD)的一个例子: 已知一个矩阵A:
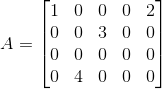
首先求出(AA转置)的值:
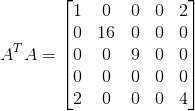
接着可以求出其特征值和相对应的特征向量:
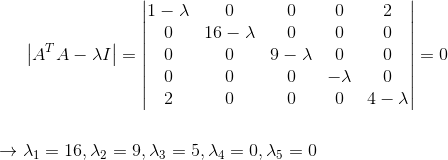
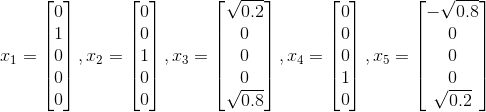
可以得到其Λ和V的值为:
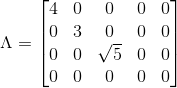
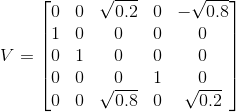
接着我们利用方法二来求U,因为λ只有三个不为0的数,根据:
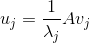
其中j=1,2,3.我们可以求出三组U的列向量:
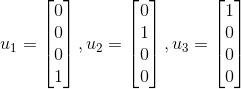
我们接着可以利用利用格拉姆-施密特正交化来补充剩余的列向量。因为A为4*5的矩阵,又Λ的大小为4*5,所以U需要4个列向量,所以需要补充一个列向量。
我们首先可以随机初始化一个4*1的列向量,比如都设为1,然后利用公式正交化得到最终结果:
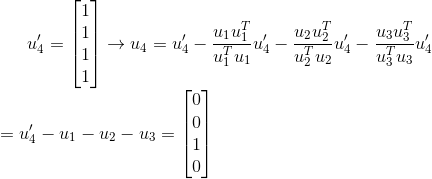
最终凑齐了4组列向量,我们得到了U:
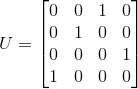
整合公式得:
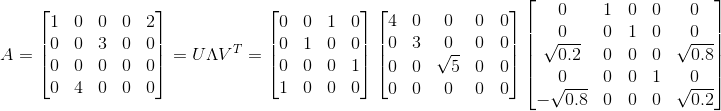
这节SVD基础篇就讲到这里,下一节讲下SVD的应用篇。