单位正交矩阵A有以下性质:
1. A转置与A相乘为单位矩阵
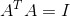
2. A转置为A的逆,由性质1就可知
3. A内的各组列向量互相正交,且每个列向量的长度都为1
那么如何让计算简单呢?比如要算最小二乘法:
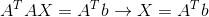
比如要算投影矩阵P:
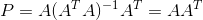
即是说,如果要对矩阵A进行处理前,先将矩阵A转换成单位正交矩阵就更有利于后期的处理。那么该如何进行转化?这里介绍一种方法——格拉姆-施密特正交化。
格拉姆-施密特正交化
讲这个方法前,得先了解投影矩阵,如果有不熟悉的可参阅什么是投影矩阵
先来看列空间为2维的矩阵的转换,已知有两条线性不相关的向量a,b,它们组成了矩阵的列空间:
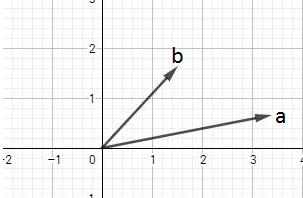
我们先确定向量a不变,然后对b做对a的投影,从投影矩阵那节得知可以求得向量e和向量p,对于投影而言,我们需要的是向量p,但对于这次而言,需要的是向量e,如图::
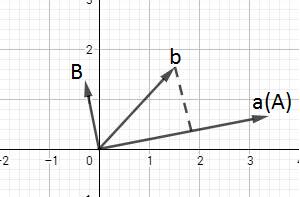
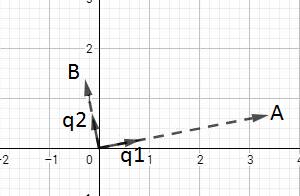
这样我们就得到两条正交的向量A和B,最后再各自分别单位化使长度为1,得到最终的结果q1和q2,其组成的矩阵Q为矩阵A转换后的单位正交矩阵:
那么公式该如何表示?首先确定一条向量,比如本次确定的是a,将其作为本次“基底”A:
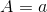
然后确定B,就是b对A做投影求B:
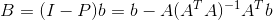
最后分别单位化得q1,q2:
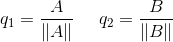
而由q1,q2组成的矩阵就是原来矩阵的单位正交化矩阵。
我们接下来看下高维的情况,以三维为例,假定有彼此线性无关的向量a,b,c,我们可以先遵循上例把A,B求出来,接下来求C:
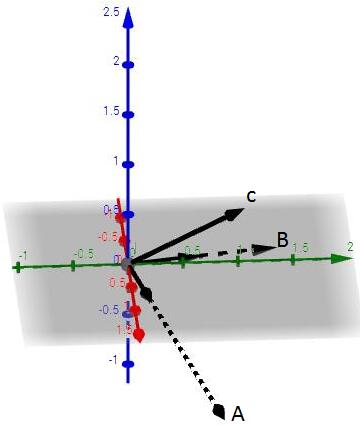
因为要保持正交,即C与A及C与B都正交,这等价于C与AB组成的空间正交,转换成求C对AB空间的投影的e向量:
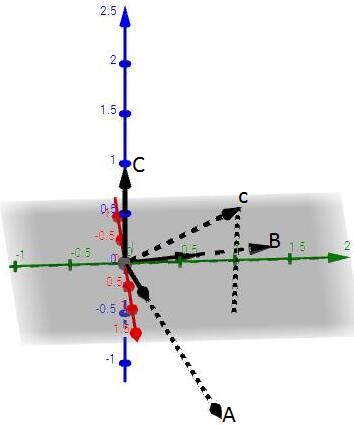
最后分别单位化即可得到q1,q2,q3:
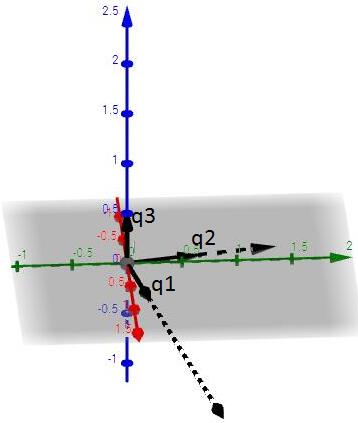
那么用公式该如何表示?首先A,B的确认跟之前一致:
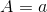
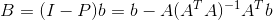
然后确定C,因为C与AB组成的平面正交,所以有:
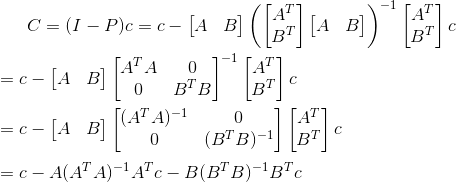
最后单位化:
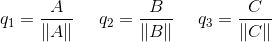
最终就得到了单位正交矩阵的全部列向量q1,q2,q3。
通过刚刚的公式推导,能得到一个一般规律:
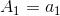
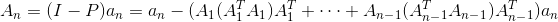
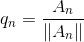
这就是格拉姆-施密特正交化。下一节,讲讲行列式