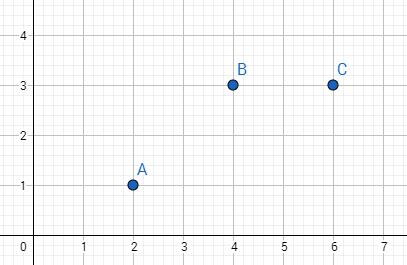
这时有人会问为什么要求一个接近的解,我们来举个机器学习常见的例子,比如有三个点A(2,1),B(4,3),C(6,3),那如果有一个点D其横坐标为7,那么其纵坐标最有可能是多少?
首先看下A,B,C的点的分布情况:
接着我们需要的是用一条直线来模拟出其点分布的趋势,那么哪条直线能更好地解释这个趋势呢?
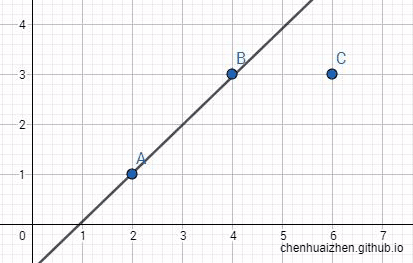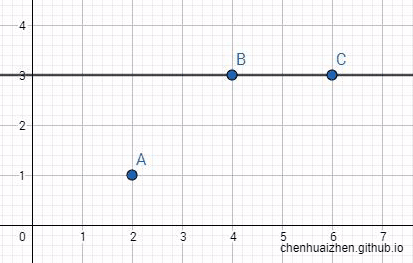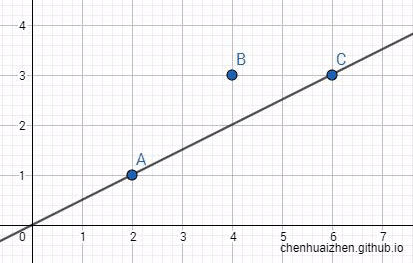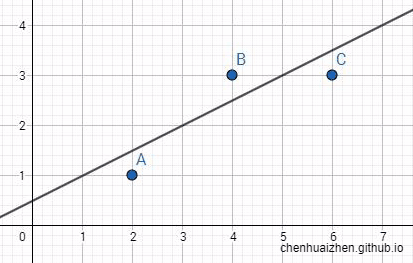
很明显的,下面这条直线最能表现出该分布的趋势:
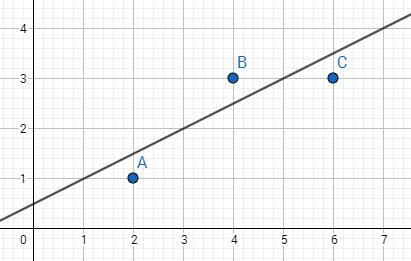
而要求该直线一般用的都是最小二乘法。就以此为例,假定直线为Y=CX+D,那么代入3组X就能求出真实值b与计算值p的误差e,如下图:
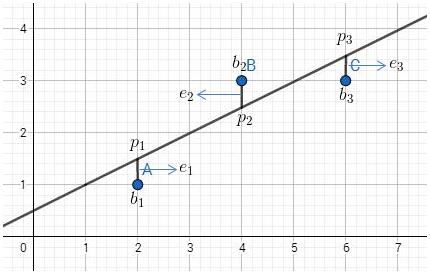
可得以下公式:
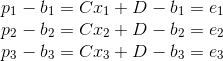
而最小二乘法要求的是f(e)的最小值:
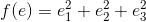
我们将x1,x2,x3代入公式,然后用高数求导的方式来求最小值:
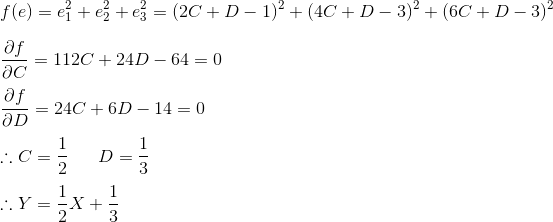
这样就把直线给求出来了。接下来我们来做一件有意思的事,我们利用上节所讲的投影矩阵来算一下这条直线如何?首先列出公式:
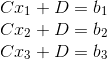
转换成矩阵形式,已知AX=b无解:
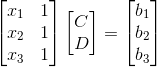
但我们知道AX=p有解:
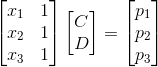
我们要做的是让e的平方和尽可能小:
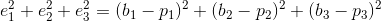
这不就是B和P点的两点距离么?
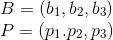
那么问题就变成了如何在空间A中找到一个点P与B点的距离最短,毋庸置疑P点是B点的投影点。那么我们就可以利用投影矩阵来算X了,分别左右各乘以A的转置来求X:
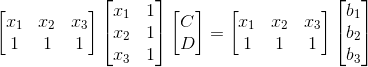
将x1,x2,x3,b1,b2,b3数值代入得:
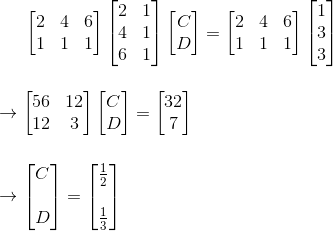
与求导出来的结果一样!所以最小二乘法可以利用投影矩阵公式来计算出最优直线,也就是求出以下的解:
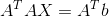
最后再强调一点,e=(e1,e2,e3)与p正交,e与矩阵A正交,如图就可以看出:
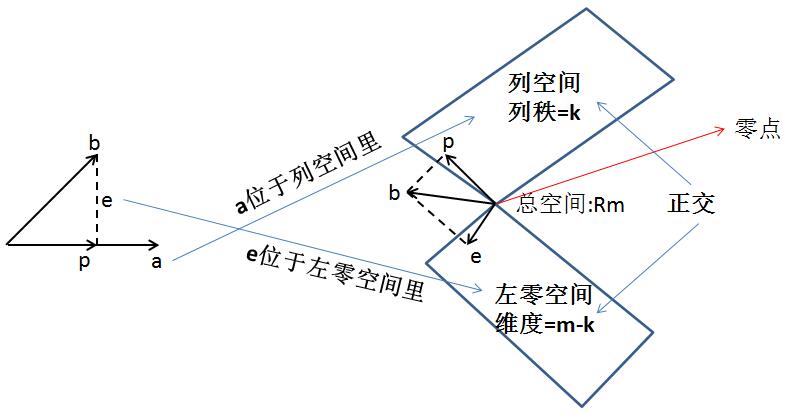
ok,下一节再来介绍个特殊的矩阵——单位正交矩阵。