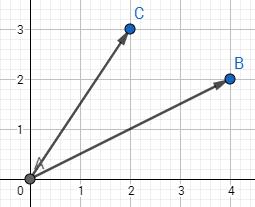
我们先来看两条向量的投影问题,假设有向量AB和AC:
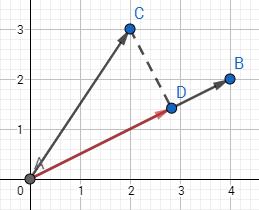
那么AC投影到AB上的向量,就是过C作AB的垂线,AD就是AC投影到AB上的向量。
这时向量DC垂直于AB,有:
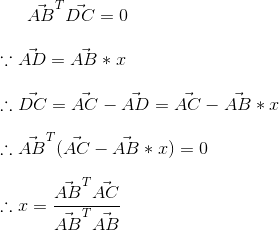
求出来的x就是AD占AB的比例,所以AD就求出来了:
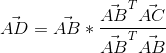
这时,我们对这个结果进行一点转化:
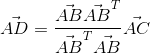
我们只是用了乘法结合律,结果就变成了一条很神奇的公式。这时,我们将矩阵P称为投影矩阵(为什么是矩阵?分母是个常数,分子是一列向量乘以一行向量,得到的结果不就是2*2的矩阵):
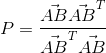
这个矩阵具有两个重要的性质,一是其转置等于本身:
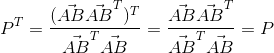
二是其无论乘以多少个本身结果都是本身,这点不难理解,对向量AC投影一次得到了向量AD,那么再对向量AD投影一次得到了什么?还是AD!无论投影多少次都是AD。这里证明平方的情况:
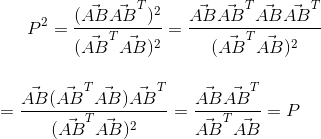
以此类推,无论投影多少次都等于本身。
接下来我们看下高维点的情况,在一个三维空间中,如何将点投影到一个面上去。
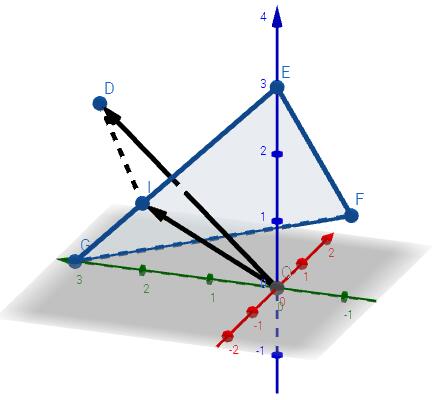
如图,已知点D,平面FGE,要想对点D做一个投影到平面FGE上,首先在D点做一垂线DI垂直平面FGE,而I点就是D点在平面上的投影,那么I点如何求?
按照上个例子的做法,已知向量ID垂直于平面FGE,我们假设平面FGE由两条线性无关的向量FE和FG组成,所以平面可以表示成(向量可看成矩阵的列向量)
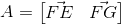
那么有:

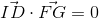
整合成矩阵可得
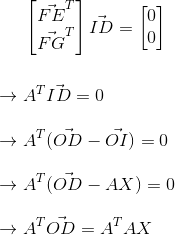
如果矩阵A可逆(如何判断矩阵可逆,可参考矩阵可逆?),那么A的转置乘以A也可逆。那么结果可化成
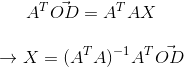
可得投影矩阵P为:
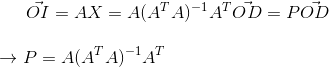
对比下向量的投影矩阵,是否十分相似:
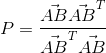
那么对于矩阵A的投影矩阵P,是否跟向量的投影矩阵一样有那两个性质呢?
首先还是P的转置等于P:
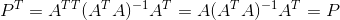
接着P的平方等于P:
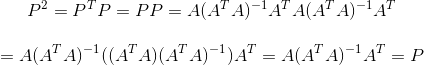
那么对于更高维的呢?跟三维的一致。已知有一空间为A,那么点D在空间上的投影是多少?令A为:
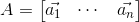
那么点D与投影到空间A上的点I之间的向量正交于空间A。有:
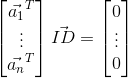
跟三维空间时一致的论证:
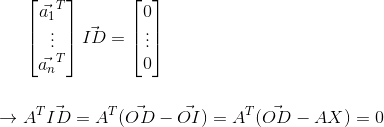
同样,如果矩阵A可逆,那么投影矩阵P为:
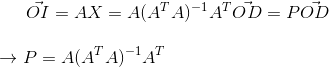
如果矩阵A不可逆,那其投影矩阵怎么求?我觉得可以先将矩阵A中线性相关的向量去掉,那么这样矩阵A就是可逆矩阵了,而且其列空间没变,其投影矩阵也不会变。
现在,我们已经得到了矩阵A的投影矩阵P,那么现在有两个特殊问题需要解决,一是如果需要投影的空间正好存在于矩阵A的列空间里,那么其投影为?假定需要投影的空间为b,其投影为b',那么有:
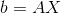
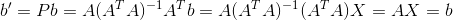
很明显,如果本来要投影的空间正好在矩阵A的列空间里,那么无论怎么投影都是其本身。
接下来是另一个问题,如果要投影的空间b正交于矩阵A,那么b与A的列空间正交,那么其投影b'为:
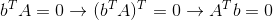
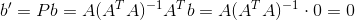
这个比较难想象了,但是如果考虑一下左零空间的概念(如果不知道什么是左零空间,可以参阅矩阵的四大子空间),如果b正交于A的列空间,那么b不就存在A的左零空间里了,那么其投影肯定为0。
下面结合之前讲过的子空间的那张图来分析下:
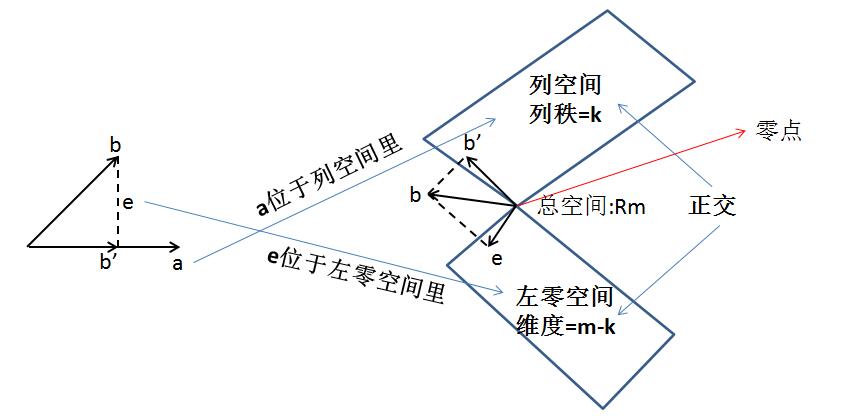
对于一个空间b,其投影到矩阵A列空间的b'与其投影到矩阵A左零空间的e都是属于投影。b'就是之前一直所讲的投影矩阵,e则为:
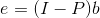
其中I-P也是投影矩阵,也满足投影矩阵的两个性质:一是转置等于本身
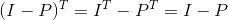
二是平方等于本身:
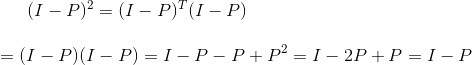
对于投影矩阵用法,下节来介绍:AX=b无解