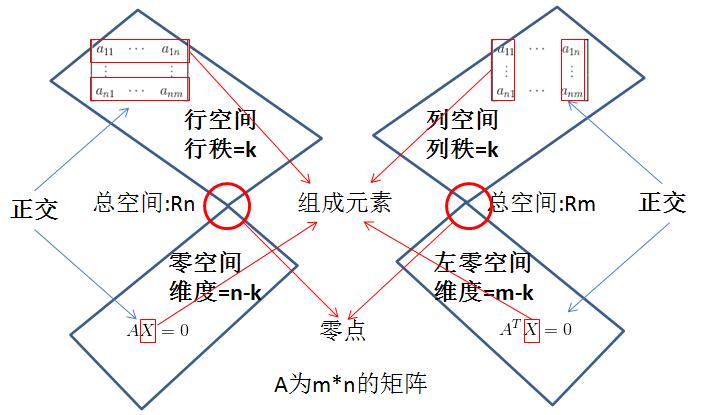
这张图顺便可以帮忙我们整理下之前所讲过的内容。
矩阵渊源
首先来看下怎么定义矩阵这么一个存在吧。直观上来看就是一组数字写在一起,可以简化方程组的运算(把变量都省去了),简化方程组可以让我们更加直观地发现构成方程组的各种元素,这样能更好发现规律。所以本人一直怀疑或许矩阵就是从方程组转换来的,后来查了下资料,发现都来自《九章算术》,再阅览了其下的《方程章》,惊奇发现原来矩阵和方程组是同时出现的。但是回想一下又不稀奇,对于方程组中的未知数,我们一直用x,y,z来标注,但对于古人来说英文字母是不存在的,那如何计算方程,直接写成矩阵形式然后用矩阵消元不就可以了?
所以矩阵最开始可以认为是用来算方程的。后来随着研究的深入才发掘出矩阵的各种性质,发展成现如今的线性代数。
向量空间
现在进入正题吧,什么叫做向量空间,向量空间的性质是什么?当空间中的任意向量相加或数乘(实数乘以向量)运算时,结果仍然在原来的空间里,这才能叫作向量空间,其是一个“封闭”的空间。同时有一点非常重要,向量空间永远都能经过零点(或零向量)
如果忘了的如何定义的话,可以参照番外篇 · 向量空间,可以知道空间的定义十分严苛,所以这四大空间的定义并不是随便定义的,而是有一定的意义才会定义出来的。
行空间
假设矩阵A为m*n的矩阵,那么我们先来看行空间。行空间,顾名思义就是矩阵每行向量所组成的空间。看到行空间,第一印象就是消元操作,毕竟消元运算是行空间的一种处理方式,也是计算AX=b的解的一种有效方法。下面是一个消元的例子:
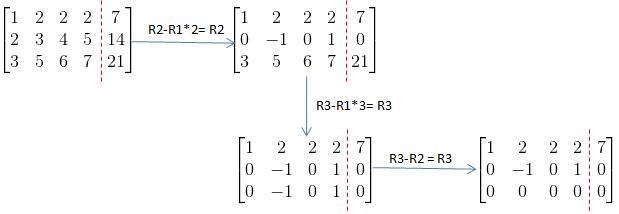
若是忘了怎么消元,可以参照消元法?矩阵转换?。
那对于AX=b什么情况下无解?这时可以从消元法上分析,可以参照下面一个例子,当b3-b2-b1=0时方有解:

对于求AX=b还有另一种形式的用法,也就是将矩阵A拆解成两个矩阵L和U,一个下三角矩阵和一个上三角矩阵,如下:
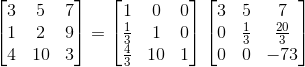
具体方法可见PA=LU?
那对于b=0,也就是AX=0时又该如何处理呢?同样是消元法,可以将矩阵逐步消元成矩阵R(左方存在一单位矩阵),如下面这个矩阵:
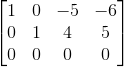
然后直接求出解空间:
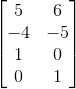
忘了怎么操作的可以参照AX=0?
零空间
讲完行空间,我们下面来看下零空间。刚刚求出AX=0的解空间,而这解空间就是矩阵A的零空间。零空间的维数大小跟自由变量的个数一致,如下例子:
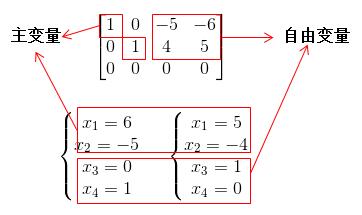
所以其零空间为:

可以知道零空间的维数为2。注意该零空间是
 的一个2维子空间。
的一个2维子空间。
行空间与零空间
这两个子空间正交,且只相交于零点。若忘记正交的定义可参照正交 = 垂直?。
这是为什么?因为AX=0。矩阵A行空间中每条向量与零空间X中的每条向量内积为0。举个例子:

那么假如行空间有一条向量T,由于在行空间上,可以表示成:
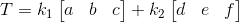
其中k1,k2为常量。再假定零空间有一条向量L,由于在零空间上,可表示成:
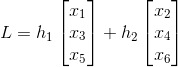
其中h1,h2为常量。那么T与L内积为:

所以很明显零空间与行空间正交。
另外,零空间的维数与行空间的维数加起来正好等于n(对于m*n的矩阵而言)。这又是为什么?下面看一张图就了解了:
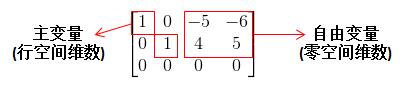
主变量个数正是行空间的维数(线性不相关的行的个数),而零空间维数正好是自由变量的个数,如果对于这些比较模糊的可以参阅AX=0?。 零空间还可以用来判断矩阵是否可逆,如果零空间维数为0那么矩阵一定可逆。如果对可逆的概念不熟悉的可参考矩阵可逆?
列空间
下面来讲讲列空间,列空间就是矩阵每列向量组成的空间。这是认识一个矩阵的基础,因为每个矩阵都可以通过列空间来查看其具体情况———将复杂的矩阵看成是多个向量的组合体可以直观地观察矩阵,可见矩阵的直观理解。
再来看AX=b这个问题吧,什么情况下有解?上面的行空间解释过了可以利用消元,这里从列空间角度出发,如果b点不在列空间里,那么AX=b无解。如下图:
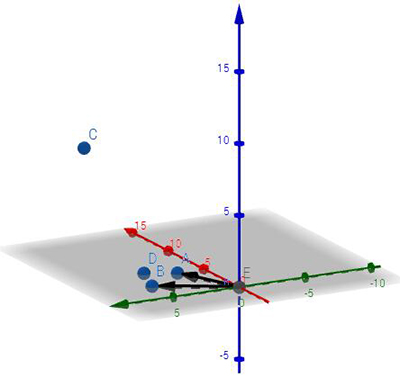
图中列空间为xy平面(图中为向量OA,OB组成),但b点(图中为点C)存在了z轴上变量,所以无解。但当b点(图中为D点)存在xy平面上时,有唯一解。
那么AX=b什么情况有唯一解,这时得从列空间的秩出发,忘了秩的概念可以查看秩的介绍
当r=n=m时(满秩矩阵),矩阵A是个方阵,AX=b有唯一解(b全都位于A的列空间里)。
当r=n<m(列满秩)时,AX=b要么无解,要么有唯一解(b落在A的列空间里才有唯一解,否则无解)。
当r=m<n时(行满秩),AX=b有无数解(b全都落在A的列空间里,但列向量个数多于列空间维数导致向量组合有无数种)。
当r<m,r<n时,AX=b要么无解,要么有无数解(b落在A的列空间里才有解,且由于列空间维数小于列向量个数,所以会出现无数解)。
具体原因忘了的话可以参照AX=b的解?
左零空间
这是个新的名词,之前没提过。但是要理解起来也不难,因为这是:
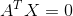
中X的空间,是不是跟零空间很像,只是零空间是左乘矩阵A,这个是左乘矩阵A的转置。那为什么叫做左零空间,因为上式左右各求转置可以化成:
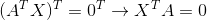
零空间是AX,是矩阵A右乘零空间X,而左零空间则反过来,是矩阵A左乘空间X,所以称为左零空间。
列空间与左零空间
这两个子空间正交,且只交于零点。具体证明可以参照上头行空间与零空间的证明,因为把矩阵A转置后,其列空间就是转置后的行空间,而左零空间就是转置后的零空间,性质一致。
同理,列空间的维数加上左零空间的维数为m,也是将矩阵A转置后按上头之前的证明就可以得知。
列空间与行空间
这两个空间的联系是矩阵的秩,行秩等于列秩,这是一定的,可参照聊聊行秩?=列秩。
至此,这个图也就讲的差不多了,下一章来看下什么是投影矩阵。