我们将该问题转换成上一节介绍的按列分割矩阵,也就是问,矩阵A的所有列向量,是否铺满了b的所有维度?
说的通透点,如果b=(x1,x2),那么b的维度就是2维平面,如果b=(x1,x2,x3),那么b的维度就是3维空间,如果b=(x1,x2,……,xn),那么b的维度就是n维空间。
首先来看2维平面的情况,如果矩阵A有两条线性不相关的列向量,那么不就能铺满一个2维平面?
什么叫线性不相关?
简单来讲,如果是2维平面,两条向量不共线就是线性不相关;如果是3维空间,3条向量不共面就是线性不相关
严谨的讲法得看定义:
如果有一组向量AB,AC,……,AN,如果存在一组不全为0的解(x1,x2,……,xn)使x1*AB+x2*AC+……+xn*AN=O(零向量),那么这组向量线性相关。如果不存在则线性不相关
如下图的向量AB跟AC,在该平面上有许多任意点(F~N),选取任意点,必定存在一个解(x,y)使向量AB和AC能够合成AF~AN
简单来讲,如果是2维平面,两条向量不共线就是线性不相关;如果是3维空间,3条向量不共面就是线性不相关
严谨的讲法得看定义:
如果有一组向量AB,AC,……,AN,如果存在一组不全为0的解(x1,x2,……,xn)使x1*AB+x2*AC+……+xn*AN=O(零向量),那么这组向量线性相关。如果不存在则线性不相关
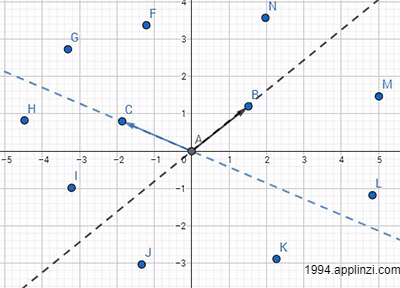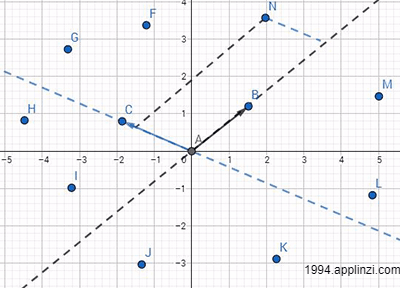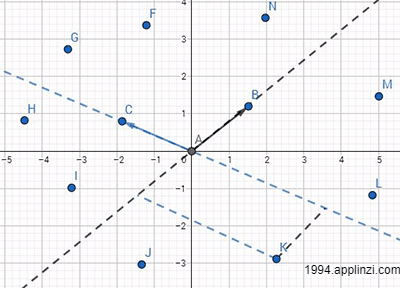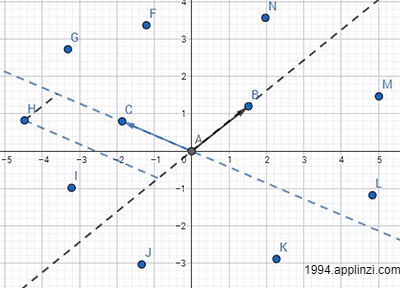
那么这不就说明向量AB和AC能够代表整个二维平面,毕竟面是由无数个点组成的。
回到矩阵上,AB和AC是矩阵A的2个列向量,也就是说矩阵A=[AB,AC](想象成2*2的矩阵)的列空间是一个二维平面。同时这个二维平面也可以称作矩阵A的值域空间。
矩阵A=[AB,AC],假定AB=(2,3),AC=(4,1),那么
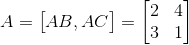
我们再来看下AX=b,如果结果b的点存在于矩阵A=[AB,AC]的列空间里,那么肯定有解,且只有一个解。如果结果b不存在矩阵A的列空间里(比如说存在在一个3维空间里),那么肯定无解。比如说下图矩阵A=[OA,OB],如果结果b在D的位置,那么有唯一解,如果b点在C的位置,那么无解。
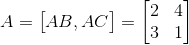
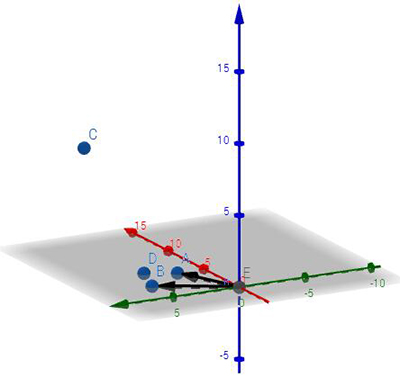
那么什么时候存在无数解?我们再来看一个矩阵A=[AB,AC,AD](想象成2*3的矩阵),AB=(1,4),AC=(3,2),AD=(-1,3),那么它的列空间仍然是一个平面。
为什么?因为三组向量都是二维的向量,缺乏第三维的位置(或者第三维位置为0),也就是说三组向量是共面的,肯定存在一组(x,y,z)使x*AB+y*AC+z*AD=(0,0)。换句话说,这三个向量线性相关。只有2个(3个中任意2个)向量线性不相关。
这时就可以引入矩阵的秩的介绍
矩阵的秩是矩阵的列秩和行秩的简称,因为行秩=列秩,所以统称为矩阵的秩。具体原因可以看番外篇:聊聊行秩?=列秩
矩阵的列秩是其列空间覆盖范围的维数,同理,行秩也是其行空间覆盖范围的维数。
比如拿上面的矩阵A为例,其列秩为2,因为其列空间只是一个二维平面;
那么对于行秩,其行空间[跟列空间类似,只是横着分割矩阵]就是向量(2,3,7)和向量(1,4,8)构成的空间,很明显只有两条向量只能构成一个二维平面(注意跟列空间的二维平面不是同个平面!)
那如果是一个4*8的矩阵,其秩是多少?
首先看矩阵的列空间,其8组向量是否线性相关,如果是,把线性相关的向量去掉(比如去掉4组),最后剩下的向量个数(4个)就是矩阵的列秩,也就是矩阵的秩=4。
同理也可以看矩阵的行空间,其4组向量是否线性相关,如果是,把线性相关的向量去掉,最后剩下的向量个数就是矩阵的行秩,也是矩阵的秩。注意,行秩一定等于列秩。
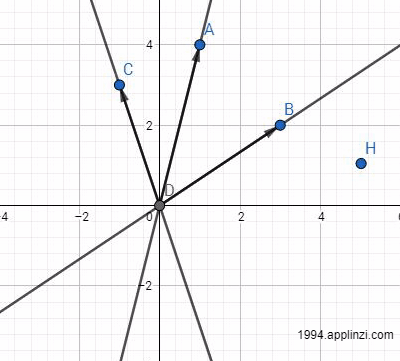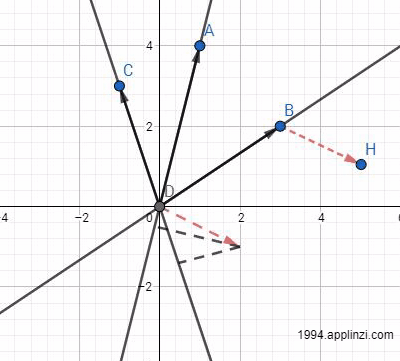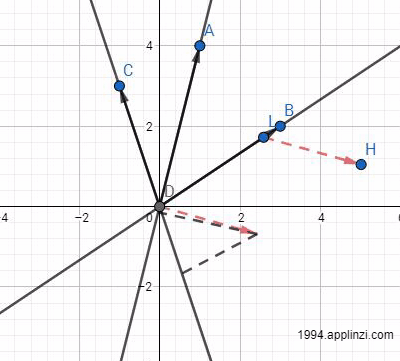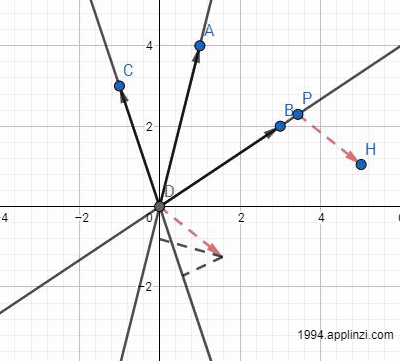
对于刚刚的矩阵A=[AB,AC,AD],如果结果b刚好落在其列空间里,这时会出现什么情况?我们可以先固定AC方向的长度,然后找到剩余的向量,再分解成AB与AD向量的结合(注:图中DB即AC向量,DA即AB向量,DC即AD向量,H即结果b位置)
矩阵的秩是矩阵的列秩和行秩的简称,因为行秩=列秩,所以统称为矩阵的秩。具体原因可以看番外篇:聊聊行秩?=列秩
矩阵的列秩是其列空间覆盖范围的维数,同理,行秩也是其行空间覆盖范围的维数。
比如拿上面的矩阵A为例,其列秩为2,因为其列空间只是一个二维平面;
那么对于行秩,其行空间[跟列空间类似,只是横着分割矩阵]就是向量(2,3,7)和向量(1,4,8)构成的空间,很明显只有两条向量只能构成一个二维平面(注意跟列空间的二维平面不是同个平面!)
那如果是一个4*8的矩阵,其秩是多少?
首先看矩阵的列空间,其8组向量是否线性相关,如果是,把线性相关的向量去掉(比如去掉4组),最后剩下的向量个数(4个)就是矩阵的列秩,也就是矩阵的秩=4。
同理也可以看矩阵的行空间,其4组向量是否线性相关,如果是,把线性相关的向量去掉,最后剩下的向量个数就是矩阵的行秩,也是矩阵的秩。注意,行秩一定等于列秩。
不难发现,随着AC(图中为DB)长度的变化,分别对应一个分解结果,也就分别对应一个解。可以预见,AC(图中为DB)方向长度的变化是无数多的,所以解也是有无数多个。
我们也可以从行空间来看,其行向量可以转成如下:
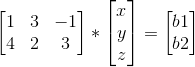
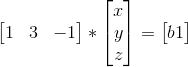
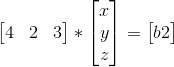
其解为两个平面的相交,两个平面相交成一条直线,即解为一条直线,所以有无数多解。
我们再从另外一方面来看这个问题。AX=b,假设A是一个m*n的矩阵,其秩为r。
当r=n=m时(满秩矩阵),矩阵A是个方阵,AX=b有唯一解(b全都位于A的列空间里)。
当r=n<m(列满秩)时,AX=b要么无解,要么有唯一解(b落在A的列空间里才有唯一解,否则无解)。
当r=m<n时(行满秩),AX=b有无数解(b全都落在A的列空间里,但列向量个数多于列空间维数导致向量组合有无数种)。
当r<m,r<n时,AX=b要么无解,要么有无数解(b落在A的列空间里才有解,且由于列空间维数小于列向量个数,所以会出现无数解)。
最后总结一番,对于AX=b,可以从行空间或列空间来看待矩阵A,再来看b所处的位置来判断是否有解。但我还是喜欢从列空间来分析其解的存在与否,同时,矩阵的秩也是判断有无解的重要标志。那如何求出解,本章没有详细介绍,欢迎看下一章节消元法?矩阵转换?