相信各位高中或初中就学过多元函数求解,其实用的都是消元法。只不过这里的表现形式从方程组变成矩阵而已。
我们先来看一组方程式:
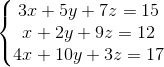
其矩阵表示形式AX=b如下:
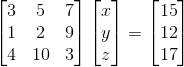
那么要求这个方程组,我们首先想到的就是消元。而最直观的想法就是从上往下逐级消元,比如第一行保留x,y,z,第二行只保留y,z,第三行只有z,这样就能逐级求出方程组的解了。放到矩阵中也是类似,我们可以把矩阵A变成一个上三角矩阵(上三角矩阵的对角线左下方的系数全部为零),其运用的也是消元的思想:
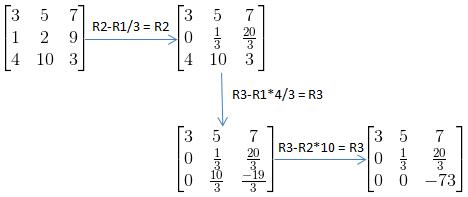
我们再来结合下输出结果b,将结果b合并到原先矩阵A后生成的矩阵叫做增广矩阵,如下所示:
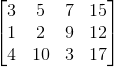
将刚刚消元的矩阵换成增广矩阵后变成:
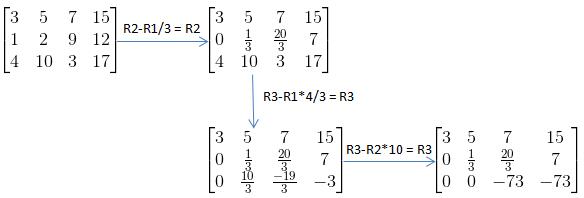
其可转换成方程组的形式:
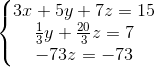
可以容易求出:
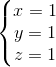
上例我们求出了一个唯一解,但上一章我们还发现有存在无数解的情况,那么这些情况该如何处理?
继续给出一个例子:
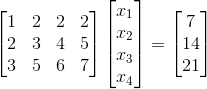
我们继续使用增广矩阵消元法来求解:
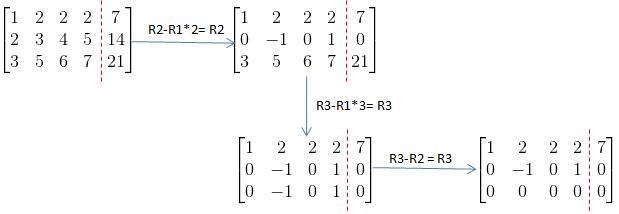
转换成方程的形式得:
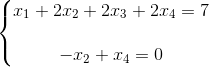
这时我们可以对X3,X4取自由值(具体原因之后会有章节会详讲,可见AX=0?),比如这里我们常用的值是都设为0。所以这里就有一组特解:
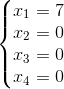
但很明显这组方程有无数个解,那么该如何来表示,这时可以让特解加上常数C倍的零解(AX=0的解),使其代表方程的实际输出。这是为什么?
原因很简单,将特解用X1表示,零解用X2表示,那么A(X1+CX2)=AX1+ACX2=b+C*0=b,所以这组解符合原方程的输出。我们再从图像的角度来分析这组解,特解X1表示的是一个向量,零解X2则表示的是一个空间。不知各位能不能想象出来,一个本来经过零点的空间(零空间必定经过零点),被向量给顶偏移了,最后那个空间就变成了AX=b的解空间。由于例子的解是4维图像比较难画,我们用一个三维空间来画图解释下:
一开始假定零空间为一平面,其必定经过零点:
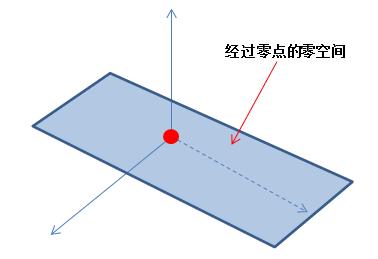
因为加了一个特解进去零空间发生了位移:

解空间上面的解都是AX=b的解,同时也符合特解加上C倍的零解这一表现形式:
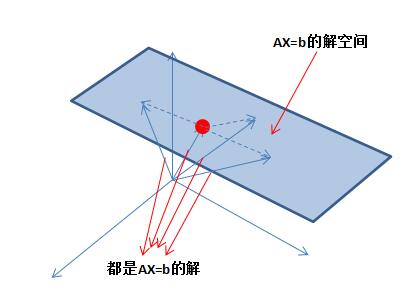
回到之前那个例子,其零解为(具体计算过程这里不讲,后面会有一个章节来进行介绍AX=0?)
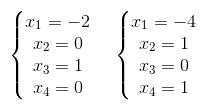
所以最后AX=b的解空间为:
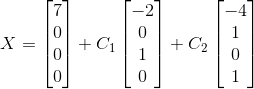
其中C1,C2都是常数,验证结果正确。
最后,我们再来看一下什么情况下无解。上一章已经通过列空间分析了无解的情况,这里我们简要通过消元计算的形式来分析无解的情况。假定有一个方程AX=b:
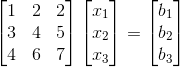
还是用增广矩阵消元得:

这时就有一个很明显的性质显示出来,如果b3-b1-b2!=0,那么这条方程无解。如果b3-b1-b2=0,那么方程有无数解(有无数解的原因可看上章内容AX=b的解?中关于解个数的分析)
在机器学习里,解方程不是重点,重点是矩阵的性质。所以我们再回过头来看刚刚那个矩阵A:
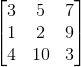
假定有一个矩阵U:
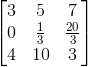
那A可以通过一个矩阵乘法转换成矩阵U么?答案是肯定可以。已知矩阵U是矩阵A的第二行减去第一行的1/3并替代第二行后得到的,那么我们的转换矩阵可以写成下面这种形式:

容易验证:
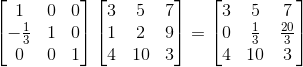
这条性质很重要,需要发动脑筋想象下具体变化过程,了解转换矩阵的用途。
接下来还有一个性质,如果矩阵U还想继续变化成矩阵V:
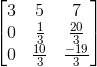
那还需要继续左乘一个转换矩阵:

可以验证:
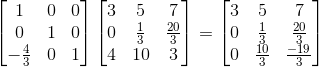
那么,有没有一个转换矩阵可以让矩阵A直接变成矩阵V,由于矩阵乘法遵循乘法结合律,所以有如下:

这时我们还会问,是否存在一个转换矩阵可以使原矩阵行顺序交换的,答案是存在的:
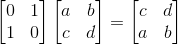
那使列顺序交换的呢?这时就不能左乘了,得右乘:
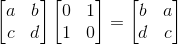
那是否存在转换矩阵不改变原矩阵的,这种转换矩阵叫做单位矩阵(n*n矩阵上主对角线上值全为1,其余值全为0):

那是否存在一个矩阵能让矩阵U回退回矩阵A呢?答案是有的,而这种矩阵与原先让矩阵A变成矩阵U的转换矩阵互为逆矩阵,对于逆矩阵的介绍,我想放到下一章节再继续,矩阵可逆?