首先来看一组方程组
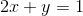
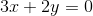
常规算法是直接消元分别求x和y,在这里我们先把它当成一个矩阵看待,以上公式可以转化成AX=b的矩阵相乘形式
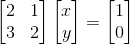
矩阵乘法运算规则,如下例子,不再赘述:
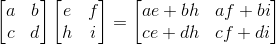
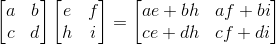
对于刚刚那个AX=b的式子,矩阵A为:
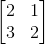
我们可以将其分成两行,再代入AX=b,可以得到如下:
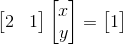
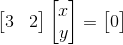
这时可以用直线图来表示,x,y分别代表直线图上的坐标,其图像如下:
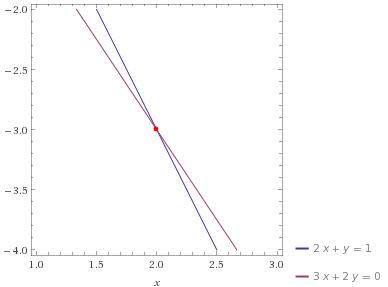
那么换种思路,我们把矩阵A分成两列,再代入AX=b,可以得到如下:
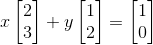
这时就不能用直线图来表示了,得改成向量表示,而x,y分别代表的是两个向量的长度,如下图:
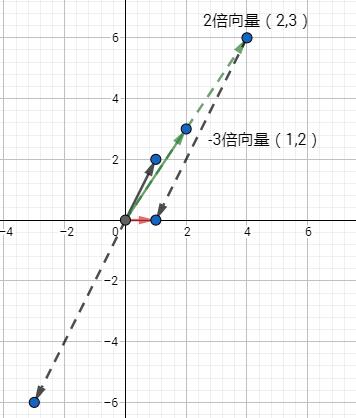
所有可以得出x,y分别为2和-3,与刚刚直线图交点一致。
那么接下来看下3*3矩阵的例子,如下有一个新的AX=b的例子:
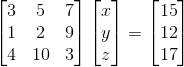
跟刚刚类似,我们先从行来分解矩阵A,再代入AX=b,得到如下:
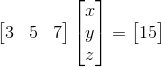
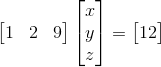
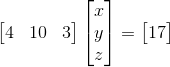
其图像是三个相交的平面,两个平面相交能够得到一条直线,那条直线再与第三个平面相交,能得到一个点,所以三个面相交能得到一个点,图如下:
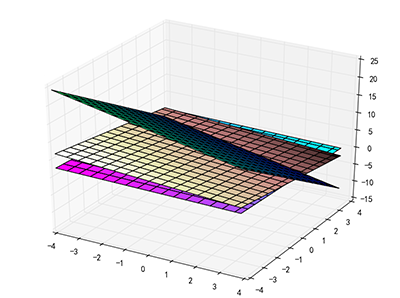
其交点为(1,1,1),我们可以验证其代入后符合AX=b
我们再用列分解矩阵A,代入AX=b,得到如下:
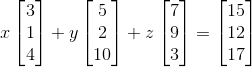
其向量表示如下图,其中向量OA为(3,1,4),向量OC为(5,2,10),向量OD为(7,9,3),向量AF为向量OC平移到以A点为起点,向量FE为向量OD平移到以F点为起点,故向量OE(15,12,17)=向量OA+OC+OD,所以x,y,z的解为分别为1,1,1,与上个图的交点位置值一致:
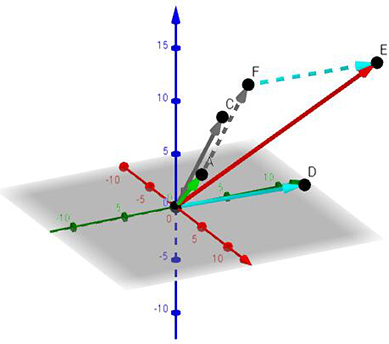
看到这里,相信各位对矩阵的横向和竖向有了直观上的认识。对于求解AX=b的问题,常用的还是按列分割矩阵。按行分割矩阵有个理解上的限制,如果矩阵的大小是4*4,那么其解的形式就不那么容易用图像表现出来,毕竟4维图像不好想象(如上例子,当矩阵大小为2*2,可以用2维平面坐标表示,当矩阵大小为3*3,可以用3维立体坐标表示)。如果按列分割,无论矩阵多大,都可看作是向量组合的形式,这样便于理解高维矩阵。
下一篇,我们来聊聊AX=b的解