向量B:

它们的内积为0:
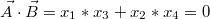
这时就说A与B正交。
看到这,相信很多人想起了垂直的概念,确实,两条向量垂直的条件也是内积为0,那么正交与垂直的区别在哪里?答案藏在了高维的空间里。
接下来推广到高维空间(不是现实中的高维空间,而是矩阵中的高维空间),两个空间A,B是正交的充要条件是A中的任意向量与B中的任意向量正交。这个条件很苛刻,一般是无法想象出来,只能靠计算才能得知,同时也是因为这个条件,所以正交跟垂直才有了本质上的区别。
举个例子,墙与地板是正交的么?答案是否定的。因为墙与地板相交于同一条向量,这条向量同时属于墙与地板,但这条向量肯定不能正交自己,所以墙与地板不是正交的。这时,是否感觉到了垂直于正交的区别。明显墙面是垂直于地板面的,因为之前高中数学有学过两个平面垂直的充要条件,就是一个平面上有一条向量(法向量)垂直于另一个平面即可。但是正交的要求是所有向量都得垂直于另一个平面,这就是区别所在。
那么再举个例子,墙上一条垂直于地板的向量于地板是正交的么?答案是肯定的。因为这条向量所构成的直线空间中,都正交与地板空间里的任意向量。
正交与垂直的区别说完了。再扯点别的吧,如何判断两个空间正交。定义已经给出,但还没论证过,为什么两向量内积为0就正交?
首先我们来到最熟悉的勾股定理,已知一直角三角形ABC:

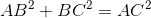
现在用向量来表示这个图:
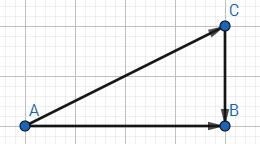
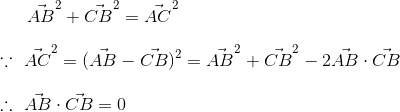
所以内积为0就代表两个向量垂直,也就是正交(因为正交是垂直的一种推广,但要切记两者是不一样的)。
换用我们之前学过的矩阵,其实内积也可以表示为矩阵的乘法:
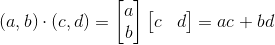
所以向量正交也可以表示为:
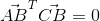
这种形式的正交也可以用勾股定理证明:


好了,有关正交的知识就暂且先告一段落,正交在矩阵尤其是机器学习中用处很多,这里只做基础介绍不展开讲,以后遇到相关问题再回头过来分析~~~下一章,讲讲矩阵的四大子空间。