三者关系
1. 矩阵的迹(trace)的和与特征值和相等
2. 矩阵的行列式值为特征值的乘积
从简单例子出发
假定有一矩阵A:
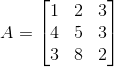
用以下公式可以求出特征值:
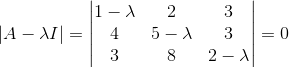
我们将上式进行分解可得:
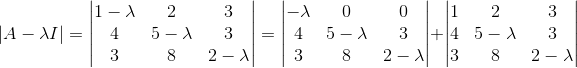

进一步求值可得:
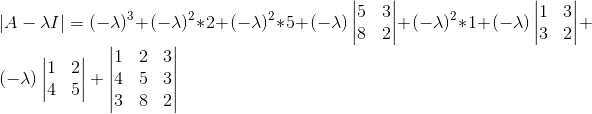
整理下可得:
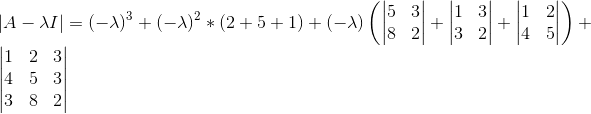
我们从另一个角度来看特征值:
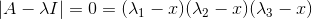
将其展开可得:
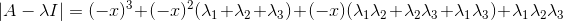
跟上式对比:
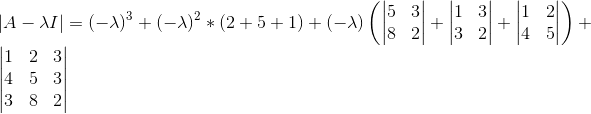
可得最开始说的关系公式:
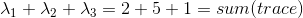

推广到n*n矩阵
按照3*3的矩阵,我们可以推出n*n的矩阵A求特征值的分解形式:
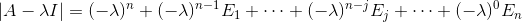
其中,Ej的定义为消掉(n-j)行和列的特征值后矩阵剩下的全部可能余子式(大小为j*j)的和,余子式的个数为
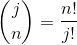
其中最特别的就是E1和En,E1为trace的和,En为行列式的值。
再从另外一个角度看n*n的矩阵A求特征值:
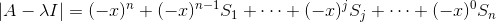
其中Sj的定义为去掉(n-j)个λ值后剩下的λ乘积的和,其个数同样是:
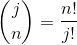
其中最特别的也是S1和Sn,S1为所有λ的和,Sn为所有λ的乘积。
对比上面两式,可以得出E1=S1,En=Sn,故矩阵的迹的和等于特征值的和,矩阵的行列式值等于特征值的乘积。