首先看下置换矩阵。通过之前章节相信各位对置换矩阵有了一定的了解,那么这时有一个问题,如果只能交换行序,那么对于一个n*n的矩阵,其总共有多少种交换方式?(可以看成是一种排序问题)
结果是n!(n的阶层)种。
换句话说,也就是有n!个置换矩阵存在,而由n!个置换矩阵组成的这组矩阵集,有个很有意思的现象,其内部的各个矩阵无论怎么相乘,或者取逆矩阵,结果都能在这组矩阵集里找到对应的解。换句话说,该矩阵集包含了该矩阵所有的行置换情况。
另外,置换矩阵还有一个重要的性质,其转置等于其逆矩阵!
举个例子证明下,对于一个2,3行置换后3,4行再转换的置换矩阵P1:
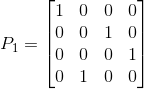
那么其逆矩阵也是置换3,4行后2,3行再转换的置换矩阵P2:
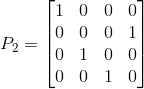
不难验证P1*P2=I,同时也可看出P2是P1的置换矩阵。
接下来讲下置换矩阵,其有一个很重要的公式:
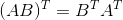
而对于对称矩阵,其转置等于本身。而更常见的形式是矩阵A乘以矩阵A的转置得到一个对称矩阵。其证明如下:
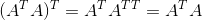
对于对称矩阵,在机器学习经常能见到,这里先不细讲,以后遇到再细讲。下一章讲讲AX=0?